Trading in the DeFi era: automated market-maker
Trading of cryptoassets in DeFi relies on new and unique matching mechanisms. One widely used mechanism in traditional finance is the centralised limit order book, which entails keeping electronic records of all outstanding orders.
Likewise, crypto centralised exchanges (CEXs such as FTX, Binance or Kraken) rely on limit order books managed off-chain. But in DeFi, the sheer volume of orders would render the management of an on-chain limit order book very costly. Another mechanism in traditional finance – the dealership model, where dealers use inventories of assets in over-the-counter (OTC) trading – revolves around establishing trustworthy relationships with counterparties. Such intermediation is not feasible in DeFi due to the anonymity of transactions, and it also goes against the stated aim of building an intermediary-free ecosystem. To dispense with limit order books and the dealership model, decentralised exchanges (DEXs) resort to so-called automated market-maker (AMM) protocols.
AMM protocols allow traders to exchange one cryptoasset for another automatically on a blockchain. They build on the idea that traders can become liquidity-providers by making their cryptoassets (eg ETH and Tether) available in liquidity pools. In turn, protocols allow other traders demanding liquidity (ie liquidity-takers) to buy or sell the cryptoassets in the pool, with relative prices set on the basis of quantities.
One popular type of AMM sets the liquidity-takers' exchange rate between token X and Y on the basis of the following constant product function that links relative prices and quantities (also known as the bonding curve):
Amount of token X * Amount of token Y = constant.
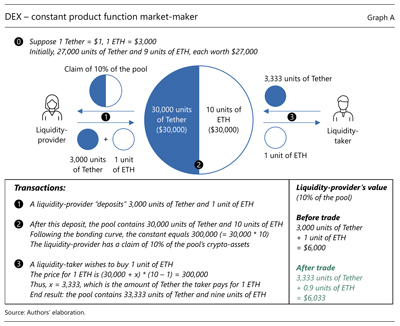
Graph A illustrates this AMM with an example of a liquidity pool comprising Tether and Ether. When a trader wishes to provide liquidity, they need to deposit Tether and Ether in proportion to the two cryptoassets' dollar values in the pool (which is one at step 
). The liquidity-provider's claim on the pool is proportional to its contribution.
The AMM protocol incentivises liquidity provision in two ways. First liquidity-takers pay to the providers a fee that may range from a few basis points to several percentage points. Second, at each extraction of liquidity, the bonding curve generates an automatic transfer from the liquidity-taker to the providers. In the example in Graph A, the liquidity-taker pays a premium to acquire 1 ETH (equal to 333 units of Tether at step 
). This makes the overall pool – and the claim of the liquidity-provider in particular – appreciate in value (bottom of right-hand panel).
That said, liquidity-providers can suffer losses if the relative price of the two cryptoassets on other exchanges diverges substantially from that implied by the bonding curve. The loss is realised when the liquidity-takers withdraw the cryptoasset that has increased in value, leaving the liquidity providers worse off than if they had kept their funds outside the pool. The transaction fees may not be high enough to offset this loss, which is commonly referred to as "impermanent loss".
Certain features of AMMs expose liquidity-takers to market manipulation on DEXs. The execution of trades in AMMs requires validations based on the blockchain's consensus protocol, ie buy and sell orders are stored in a public memory pool, so that validators (also known as "miners") can add them to the blockchain. When submitting orders, liquidity-takers are uncertain about the timing of their orders' execution and the execution prices, as these depend on the execution sequence. Importantly, the order quantities become public knowledge before their price impact has materialised – which is easily predictable from the bonding curve. This time lag opens the door to malicious activity, whereby a trader may try to place a buy and an offsetting sell order immediately before and after, respectively, the pre-announced buy order. When the latter order is large enough, the bonding curve implies that the malicious trader's sell order will be executed at a higher price than his buy order, thus generating a profit. Such front-running behaviour is particularly attractive to large validators because they have a higher chance to "win" the next block and time their front-running trades optimally. The profits sometimes are called "miner extractable value".
More and more analytical work on the pros and cons of AMMs is emerging. On the one hand, AMMs enable on-chain trading without intermediaries, improving interoperability with other DeFi platforms such as lending and investment platforms. Compared with a limit order book model, the bonding curve in AMMs also mitigates overcompetition between liquidity-providers on prices, potentially enhancing liquidity provision overall (Lehar and Parlour (2021)). On the other hand, the strict bonding curve in AMMs limits the flexibility of liquidity-providers and exposes them to impermanent losses, thus deterring traders from liquidity provision. The risk of being front-run may also push traders away from AMM protocols.
As the DeFi ecosystem remains in flux, AMM designs are still evolving. One emerging feature brings AMMs closer to the traditional limit order book model. Specifically, liquidity-providers can choose which range of the pricing curve they would like to provide liquidity to. When the transacted price falls within this range, the mechanics described above apply. Otherwise, the liquidity-providers' assets are removed from the active liquidity pool. In addition, the types of cryptoasset that can be traded via AMM protocols are also expanding, ranging from non-fungible tokens to tokenised equity shares.
The views expressed in this box are those of the authors and do not necessarily reflect those of the BIS. The AMM trading mechanism shares similarities with the framework of Shapley and Shubik (1977), which ensures market-clearing. See L Shapley and M Shubik, "Trade using one commodity as a means of payment", Journal of Political Economy, vol 85, no 5, pp. 937–68, and H S Shin, "Comparing the robustness of trading systems to higher-order uncertainty", Review of Economic Studies, vol 63, no 1, pp. 39–59. Decentralised trading is often fragmented. If there are multiple pools trading the same asset pair, one may use a smart order router for the best prices.
