CIP, FX swaps, cross-currency swaps and the factors that move the basis
(Extract from pages 48-49 of BIS Quarterly Review, September 2016)
CIP is a textbook no-arbitrage condition according to which interest rates on two otherwise identical assets in two different currencies should be equal once the foreign currency risk is hedged:
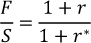
where S is the spot exchange rate in units of US dollar per foreign currency, F is the corresponding forward exchange rate, r is the US dollar interest rate, and r* is the foreign currency interest rate. In practice, the relationship between F and S is read off market transactions in FX instruments, notably FX swaps and cross-currency swaps.
In an FX swap, one party borrows one currency from, and simultaneously lends another currency to, a second party (see also Baba et al (2008)). The borrowed amounts are exchanged at the spot rate, S, and then repaid at the pre-agreed forward rate, F, at maturity. The implicit rate of return in an FX swap is determined by the difference between F and S, and the contract is typically quoted in forward points (F - S). If the party lending a currency via FX swaps makes a higher or lower return than implied by the interest rate differential in the two currencies, then CIP fails to hold. Typically, the US dollar has tended to command a premium in FX swaps. In this case, rearranging the CIP equation yields the following relationship between (F - S), r and r*:
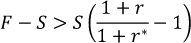
A positive ("wide") value of (F - S), above, indicates that a party lending US dollars sells the foreign currency forward at a higher dollar price than warranted by the interest differential. Equivalently, a party borrowing US dollars via an FX swap - say, to hedge its US dollar asset - is effectively paying a higher interest rate on the swapped dollars than is paid in the cash market.
A cross-currency swap is a longer-term instrument, typically above one year, in which the two parties also simultaneously borrow and lend an equivalent amount of funds in two different currencies. At maturity, the borrowed amounts are exchanged back at the initial spot rate, S, but during the life of the swap the counterparties also periodically exchange interest payments. In a cross-currency basis swap, the reference rates are the respective Libor rates plus the basis, b. Again, if the forward points (F - S) are greater than warranted by CIP, then, assuming a one-period maturity, the basis, b, will effectively be the amount by which the interest rate on one of the legs has to be adjusted so that the parity with the pricing of FX swaps holds:
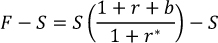
In the above example, the FX swap implied US dollar rate, F⁄S(1 + r*), exceeds actual US dollar Libor, 1 + r, if the party borrowing US dollars in a cross-currency swap pays the basis, b, on top of US dollar Libor. Thus, failure of CIP has implications for the relative cost of funding in the cash and swap markets. Whenever CIP fails, one party ends up paying the currency basis on top of the cash market rates to borrow the corresponding currency, while the other counterparty in effect receives an equivalent discount when borrowing the other currency.
A number of factors can cause CIP to fail. For example, market liquidity in the underlying instruments may evaporate, so that the difference between bid and ask prices for forward and spot transactions is non-trivial. For simplicity, let us assume that r* is sufficiently small, so that 1 + r* ≈ 1. Denoting by Sa the spot ask rate and by Fb the forward bid rate, CIP deviations due to a drop in market liquidity will be given by:
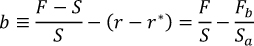
CIP can also fail because of credit risks in the underlying investments. If CIP arbitrage is conducted by global banks borrowing and lending in the respective Libor markets, then a rise in counterparty credit risks in the interbank markets, typically captured using Libor-OIS spreads, could result in CIP deviations. Similarly, if banks or asset managers engage in CIP arbitrage using government bonds in the two currencies, then deviations might result from differences in sovereign credit risks, typically measured using sovereign CDS spreads.
More generally, suppose r and r* are the respective risk-free rates and rp is the risk premium for the underlying investment over the duration of the swap. Then CIP deviations measured using risk-free rates will be given by:
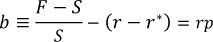
Even if risk premia in the underlying transaction are low, CIP deviations can arise if the demand to hedge one of the currencies is large. Then, even small risk premia can have big effects when scaled by the large size of the balance sheet exposures needed to meet the hedgers' demand. For example, Sushko et al (2016) show that CIP deviation can be proportional to the hedging demand multiplied by the per-dollar balance sheet costs of FX derivatives exposures:
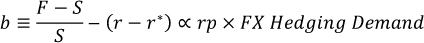
In each of the above examples, the price that is actually set in FX derivatives is that of the forward leg of the swap, F. As shown, CIP arbitrageurs will pass on their balance sheet costs of taking the other side of FX hedging demand via FX swaps as wider forward points, (F - S), than warranted by CIP. The per-dollar balance sheet costs themselves are represented by rp in this example. Since markets have to clear, the aggregate position of CIP arbitrageurs when the US dollar is at a premium in FX swaps will be equal to the aggregate net position of currency hedgers. The latter will be paying the forward points, (F - S), to hedge their US dollar assets.
What are some of the real-world counterparts to rp in non-crisis times? In aggregate, rp will reflect any costs that banks or other participants assign to deploying their balance sheet in CIP arbitrage, which in turn will reflect their risk management practices. For individual players, these practices may even include absolute credit limits that would set a maximum for the underlying exposures to the underlying instruments and counterparties. Even without strict limits, the funding cost of the capital allocated to the arbitrage activity, notably to the (current and potential future) derivatives exposures involved, will prevent the basis from closing when it opens up owing to changes in hedging demand.
The specific constraints, and hence the instruments involved, will also depend on the players acting as arbitrageurs. For instance, for highly rated supranational and quasi-government agencies, which can arbitrage the long-term basis thanks to their top credit rating by issuing bonds in US dollars at attractive rates and then swapping them out, rp is more closely related to the costs of placing bonds in different currencies. For hedge funds, which rely on collateralised markets to fund CIP arbitrage, the price and availability of repo market funding will play a significant role.
