Cointegration of policy and lending rates
(Extract from page 63 of BIS Quarterly Review, September 2013)
The results reported in Graph 1 can be formalised by resorting to an econometric model which links lending rates to other interest rates in a cointegration framework. We estimate separate models for each country under scrutiny. The specification we adopt for euro area countries is:
rl = α + βrb + e,
while for the United States and the United Kingdom it is
rl = α + βrb + γrg + e,
The rationale for including government bond yields in the specification is that failing to do so would neglect the potential impact of large-scale asset purchases implemented by the Federal Reserve and the Bank of England. Estimation is performed using the fully modified OLS estimator proposed by Phillips and Hansen (1990).1
To pin down the level of bank lending rate that would have prevailed, given the current monetary policy stance, if the pass-through had worked as in the pre-crisis period, we first estimate cointegrating equations up to August 2008. We acknowledge that the sample is short and only covers a period of strong economic and financial expansion; results should therefore be taken as illustrative.
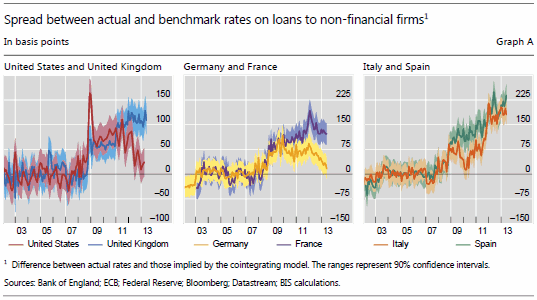
We then compute the fitted values for the rate on loans to non-financial firms, and interpret these as benchmark rates, ie the rates that would have prevailed given the current monetary policy stance had the passthrough worked as in the pre-crisis period. To gauge the deviation of actual rates from the medium-run benchmark level, we subtract the fitted values from the actual (observed) values for lending rates. Results are reported in Graph A, and basically convey the same message as the informal analysis in Graph 1.
The fact that the difference between actual and fitted values drifts away from zero constitutes indirect evidence that the relationship tying together lending and policy rates has been subject to a structural change since the onset of the Great Recession. Of course, given the coverage of our sample, such change could be due to the economic downturn itself rather than some other form of impairment in the transmission of monetary policy.
1 Further details on the coefficient estimates and cointegration tests, as well as on the stability of the cointegrating relationship, arecontained in a companion working paper (Illes and Lombardi (2013)).